[MobiSys 2022] mGEMM: Low-latency Convolution with Minimal Memory Overhead Optimized for Mobile Devices (2)

# 세미나를 위한 논문 읽기

# 2022  MobiSys에서 발표된 논문

# 오역이 있을 수 있습니다.

# 2022 08 30 seminar

 

# ACM reference Format : JongseokPark,KyungminBin,andKyunghanLee.2022.mGEMM:LowlatencyConvolutionwithMinimalMemoryOverheadOptimizedforMobile Devices.InThe20thAnnualInternationalConferenceonMobileSystems, ApplicationsandServices(MobiSys’22),June25–July1,2022,Portland,

https://dl.acm.org/doi/10.1145/3498361.3538940

mGEMM | Proceedings of the 20th Annual International Conference on Mobile Systems, Applications and Services

 

https://strangecat.tistory.com/71 ( 1 ) 

 

##

FFT (Fast Fourier Transformation)? : 

https://restudycafe.tistory.com/563

[C++ 알고리즘] 고속 푸리에 변환(FFT) (원리, 예제 코드, 응용문제 풀이)

이산 합성곱을 O(N log N) 시간에 계산

 

Winograd Transformation? :

https://medium.com/@dmangla3/understanding-winograd-fast-convolution-a75458744ff

Understanding ‘Winograd Fast Convolution’

https://aifpga.tistory.com/entry/Fast-Algorithms-for-Convolutional-Neural-Networks

Fast Algorithms for Convolutional Neural Networks

천천히 자세히 읽어봐야 함. 이해하는데 좀 걸림.

6mul 4 add -> 4mul 6add 로 변환 가능 따라서 시간 복잡도가 낮아지며 속도가 빨라질수 있음을 추론 가능하다.

 

tensor? :

https://finnsplace.tistory.com/21 참고

 

##

 

2 BACKGROUND

GEMM에 대해 알아보기 전에 GEMM 기반 방법이 컨볼루션의 지배적인 솔루션으로 사용되는 이유에 대한 배경을 제공한다.

2.1 WHY GEMM?

신경망에서 컨볼루션 레이어의 계산을 가속화하는 몇 가지 다른 접근법이 있다. FFT(Fast Fourier Transformation)[28] 또는 Winograd Transformation[25]과 같은 수학적 변환은 계산 복잡성을 줄임으로써 합성곱 연산을 가속화한다. 불행히도, 이러한 변환 기반 접근 방식은 유연성이 부족하며[20, 35] 변환 프로세스는 계산과 메모리 모두에서 오버헤드를 유발한다[25, 32]. 이러한 한계와 오버헤드를 고려할 때, 복잡성을 줄이는 접근 방식은 특히 워크로드 크기가 작은 모바일 플랫폼에서 메리트가 낮아지고 있다[52]. 더 인기 있는 접근 방식은 행렬 곱셈(GEMM)을 통한 것이다. 이 접근 방식에서 convolution tensors 와 demensions 을 행렬로 매핑된 다음 high-performancce BLAS 라이브러리[1, 5]로 파이핑된다. 컨볼루션 연산에 대한 수정은 다양한 매핑 패턴으로 매핑 프로세스에 쉽게 통합될 수 있다. 이 접근 방식의 주요 이점은 변환된 텐서를 주어진 플랫폼의 BLAS 라이브러리에 파이프함으로써 GEMM 커널이 제공하는 높은 계산 처리량을 쉽게 활용할 수 있다는 것이다.

 

2.2 The GEMM operation

 

Figure 2

 

GEMM 연산은 M, N, K의 3가지 계산 차원에 대한 중첩된 루프에서 multiply-accumulate (MAC) 연산으로 표현된다.i, j, k는 각각 M, N, K 위의 반복자이고, A(i,k), B(k,j), C(i,j)는 각각 행렬 A(M×K), B(K×N), C(M×N)의 원소이다. 이 연산은 두 벡터 집합 사이의 독립적인 내부 곱셈 계산 집합으로 이해될 수 있으며, 이는 병렬화와 데이터 재사용을 위한 큰 기회를 제공한다. 예를 들어, Figure 2에서 각 출력 요소 C(i, j)가 열 벡터 B(:, j)와 행 벡터 A(i,:)의 내부 곱으로 계산되는 것을 관찰할 수 있다. 다른 연산에는 출력 요소가 필요하지 않기 때문에 여러 출력 요소를 병렬로 계산할 수 있다. N차원에 걸쳐 출력 요소의 계산을 병렬화하면, 행 벡터 A(i,:)가 계산 간에 공유되어 병렬 계산 단위 간에 데이터를 재사용할 수 있다. 데이터 재사용은 내적 차원 K에 대해 출력 요소 C(i,k)를 재사용함으로써 단일 계산 단위 내에서 존재한다. 서로 다른 피연산자 행렬과 계산 차원에 걸쳐 많은 양의 병렬화 및 데이터 재사용 기회가 존재한다는 것을 쉽게 관찰할 수 있다. 기존 GEMM 계산 연구[8, 13, 14, 27, 41]와 라이브러리[21, 33, 50]는 기본 하드웨어의 메모리 계층 및 벡터 처리 기능의 가장 효율적인 사용을 용이하게 하는 방식으로 작업을 신중하게 분할하고 스케줄링함으로써 이러한 기회를 활용한다.

 

2.3 Mapping convolution into GEMM

고도로 최적화된 BLAS 라이브러리의 이점을 활용하기 위해서 먼저 컨볼루션 텐서를 행렬에 매핑하고 컨볼루션 계산을 행렬 곱셈에 매핑해야 한다. 

 

Notations :

우리는 convolution tensor 를 Feature Map 이나 Kernel 대신 input, filter, output 으로 지칭할 것이다. 입력 및 출력 텐서 치수는 해당 텐서의 배치, 채널, 높이, 폭 치수에 해당하는 B, Cin, Hin, Win 및 B, Cout, Hout, Wout으로 각각 표시된다. 마찬가지로 필터 텐서 치수는 Cout, Cin, Hfil, Wfil로 표시된다. 컨볼루션 연산은 알고리즘 1과 같이 입력, 필터, 출력 텐서의 요소를 피연산자로 하여 7차원 이상의 루프에 대해 중첩된 MAC 연산으로 표현될 수 있다.

Difficulties :

두 연산 모두 두 개의 입력 피연산자와 한 개의 출력 피연산자에 걸쳐 작동하기 때문에 텐서를 행렬에 매핑하는 것은 쉽다. 우리는 출력 텐서를 행렬 C에, 입력 텐서를 행렬 B에, 필터 텐서를 행렬 A에 매핑한다. 입력 및 필터 텐서의 매핑은 임의이며 교환할 수 있다. 행렬에 매핑된 후 총 계산 수는 동일해야 하므로, 모든 컨볼루션 치수 크기의 곱은 GEMM 치수의 곱과 같아야 한다. 이것은 우리의 매핑 과정 중에 컨볼루션 dimensions이 평평하게 하고 GEMM dimensions 사이에 분포해야 한다는 것을 의미한다.  그러나 이것은 피연산자를 매핑하는 것보다 더 까다롭다. dimensions 과 operand 사이의 관계가 존중되어야 하기 때문에 임의의 컨볼루션 dimension을 행렬 dimension에 매핑할 수 없다. 그렇지 하지 않는다면, 매핑된 dimension 이 잘못된 operand 에 대해 반복되어 잘못된 계산을 하게 된다. 정확한 결과를 얻으려면 7개의 컨볼루션 dimensions 와 3개의 GEMM dimensions 이 피연산자와 어떤 관계를 가지고 있는지 식별하고 동일한 관계로 dimension를 매핑해야 한다. 

 

## ex )

이건 전에 포스팅한 GEMM 을 보면 알 수 있다. 

https://strangecat.tistory.com/56?category=998875 

GEMM : C로 구현해보자!

본문에선 7중 포문이라 했는데, batch 를 포함하였기 때문.

GEMM 은 행렬 곱이기 때문에 3중 포문으로 구성되는데, 7중 포문 합성곱을 임의로 매핑하면 잘못된 계산이 되기때문에 이를 잘 맞추어 매핑 해주어야 한다.

 

## ex) end 

 

Relationship between dimensions and operands :

먼저 dimension 과 oprand 사이의 관계를 재사용 또는 액세스로 분류한다. 액세스 차원은 MAC 작업에서 주어진 operand 의 요소를 결정하는 데 관련된 dimension이다. 반대로 재사용 dimension 은 관련되지 않은 dimension 이다.

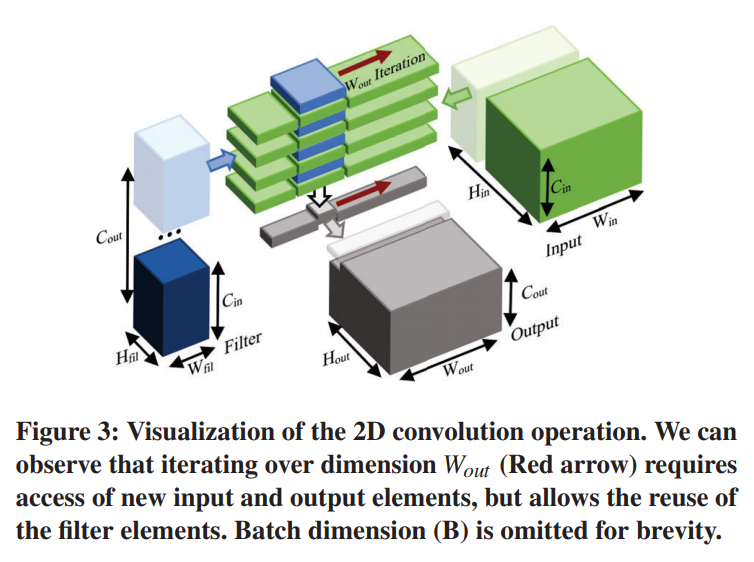
예를 들어, 그림 2에서 K 차원을 반복하면 동일한 출력 요소 C(i, j)를 재사용할 수 있는 반면 새로운 입력 및 필터 요소에 대한 액세스가 필요하다는 것을 알 수 있다. 따라서 차원 K는 출력 행렬의 재사용 차원이 되고 입력 및 필터 행렬의 액세스 차원이 됩니다. 같은 방식으로, 그림 3에서 dimension Wout을 반복하면 동일한 필터 요소를 재사용할 수 있는 동시에 새로운 입력 및 출력 요소에 대한 액세스가 필요하다는 것을 알 수 있습니다. 치수 Wout은 필터 텐서의 Reuse 차원일 수 있고, 입력 및 출력 텐서의 Access 차원일 수 있다.

 

Figure 3

GEMM과 컨볼루션 모두에서, 우리는 MAC 계산에 사용되는 입력, 필터 및 출력 요소가 계산 차원에 해당하는 iterators 의 set 에 의해 결정된다는 것을 관찰할 수 있다. 이를 참조로 사용하여 차원이 주어진 피연산자의 요소를 결정하는 데 관여하는지 여부를 쉽게 확인할 수 있다.

 

표 1은 각 텐서와 매트릭스의 접근 및 재사용 dimensions 를 보여준다. 입력 텐서에 관한 관계를 제외하고 대부분의 접근과 재사용 관계는 계산 알고리즘을 참고하여 확인할 수 있다. 다음의 분석을 위해, 우리는 입력 텐서의 Reuse 차원을 C(out), H(fil), W(fil)로 하고, Access 차원은 B, C(in), H(out), W(out)로 둔다. 이것은 입력 요소가 필터의 모든 공간 요소에 의해 방문되는 컨볼루션의 일반적인 경우에 기초한다. 우리는 이 관찰을 기반으로 알고리즘의 일반적인 구조를 분석하고 구축하며, 섹션 4의 세부 구현 단계에 입력의 정확한 관계를 통합한다.

 

Mapping computation dimensions :

표에서 dimensions B, H(out) 및 W(out)가 GEMM dimensions N과 동일한 관계를 공유하며 출력 및 입력 피연산자의 액세스 dimensions 및 필터 피연산자의 재사용을 쉽게 식별할 수 있다. 이를 통해 dimensions B, H(out)를 직접 매핑할 수 있다.열거된 차원에 의해 지배되는 요소와 계산은 N에 매핑될 때 동일한 패턴을 따르므로 N 차원으로 이동한다. 같은 방식으로 C(out)을 M에 매핑할 수 있고 C(in)을 K 차원에 매핑할 수 있다. 그러나 공간 필터 치수인 H(fil)와 W(fil)는 두 피연산자의 재사용 치수인 반면, GEMM 치수 M, N, K는 각각 하나의 피연산자의 재사용 치수이기 때문에 GEMM 치수 중 어느 것에 매핑될 수 없다.

 

2.4 Existing Implementations

공간 필터 치수의 문제를 해결하고 행렬 곱셈을 사용하여 컨볼루션 연산을 성공적으로 계산하기 위해 수년 동안 다양한 접근 방식과 구현이 제안되었다.

 

Im2col (Image to Column) :

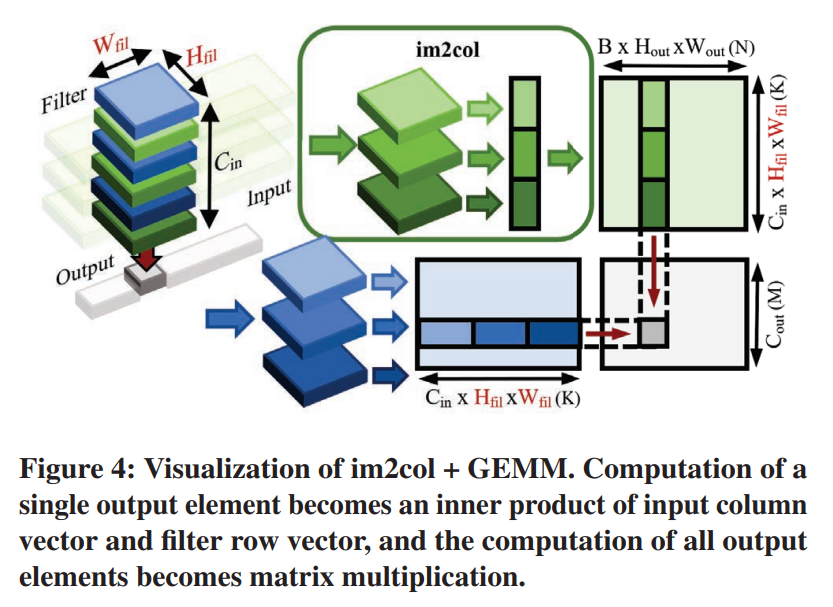
가장 널리 사용되는 접근 방식 중 하나는 im2col[5]이다. Im2col은 단일 출력 요소 계산에 필요한 모든 입력 요소를 C(in) ×H(fil) ×W(fil) 크기의 열 벡터로 평면화한다. 대응하는 평면화된 필터 행 벡터를 사용하여 단일 출력 요소의 계산은 이제 입력 열과 필터 행 벡터의 내적이다. 이것이 모든 C(out) × B × H(out) × W(out) 출력 요소에 대해 반복될 때 내적 계산의 결과 집합은 그림 4와 같이 행렬 곱셈의 형태를 취한다.

불행하게도, 각 입력 요소는 H(fil) × W(fil) 이웃 출력 요소 계산에 걸쳐 재사용되기 때문에, 입력 행렬의 열 벡터들 사이에 동일한 입력 요소의 중복 항목이 존재한다. 이것은 입력 매트릭스 크기가 원본보다 H(fil) × W(fil)배 더 커지도록 강제한다.

Im2col은 H(fil) 및 W(fil) 차원에서의 입력 요소의 재사용을 메모리 내의 분리된 중복 항목으로서 표현하고 H(fil), W(fil) 차원 및 재사용에서 액세스로의 입력의 관계를 수정하는 것으로 이해할 수 있다. 이렇게 하면 H(fil)와 W(fil)를 매트릭스 차원 K에 매핑할 수 있는데, 이는 이제 입력과 필터의 Access 차원인 동시에 출력의 Reuse 차원인 동시에 K 매트릭스 차원처럼 출력의 Reuse 차원이다. 그러나 입력 항목을 복제하면 입력 행렬의 설치 공간이 원래 텐서의 H(fil) × W(fil) 배가 될 뿐만 아니라 이러한 메모리 설치 공간과 대역폭 모두 강조하는 차원이 제공하는 입력 데이터 재사용 기회를 제거한다.

 

Im2col Optimization :

MEC[6], Indirect Convolution[9] 및 Implicit GEMM[34, 46]은 모두 im2col을 기반으로 하며, 메모리 중복 및 im2col의 재정렬의 영향을 줄이기 위한 다양한 기술을 제안한다. MEC는 H(out) 차원에서 im2col 행렬의 중복 부분을 제거하는 것을 목표로 하고 있으며, Indirect Convolution에서는 요소를 복제하는 대신 요소에 대한 포인터를 사용한다. Implicit GEMM은 일반적으로 높은 대역폭의 개인 메모리 크기로 im2col 입력 행렬의 작은 부분만 생성하고 프로세스를 행렬 패킹과 인터리빙하여 오버헤드를 숨기려고 한다. Implicit GEMM은 엔비디아의 cuDNN[34]이 배포하는 합성곱 방식이고 Indirect GEMM은 구글의 XNNPACK[12] 라이브러리를 배포하는 방식이다. 이러한 모든 방법은 오버헤드 및 처리량 손실을 어느 정도 줄입니다. 그러나 이러한 문제를 완전히 제거하는 방법은 없으며, GEMM의 낮은 데이터 재사용률은 모바일 환경에서 여전히 심각한 문제로 남아 있다. 

 

Kn2col (Kernel to Column):

im2col과 유사하게, Kn2col[1]은 출력 텐서와 H(fil) 및 W(fil)의 관계를 수정하여 출력 텐서의 재사용에서 접근으로 이동시킨다. 이를 통해 H(fil)와 W(fil)를 매트릭스 차원 M에 매핑할 수 있다. 그러나 이 과정에서 kn2col은 출력 매트릭스 풋프린트를 원래 텐서의 H(fil)×W(fil)배로 증가시키고 출력 데이터의 데이터 재사용 기회를 제거한다.

 

Direct convolutions:

직접 컨볼루션 접근법[11, 52]은 계산을 외부 행렬 곱셈 루틴에 연결하는 대신 직접 컨볼루션 계산을 주장한다. 그러나, 그들의 계산 알고리듬을 자세히 살펴보면, 그들의 계산도 행렬 곱셈을 기반으로 한다는 것이 밝혀졌다[11, 52]. 본질적으로, 이러한 접근 방식은 H(fil) 및 W(fil) 차원에 걸쳐 컨볼루션 계산을 분할하는 것이다. 이를 통해 각 파티션은 GEMM에 직접 매핑할 수 있는 C(out), C(in), B, H(out), W(out) 차원만으로 구성될 수 있다.

이러한 분할 방식은 im2col과 kn2col이 H(fil)와 W(fil) 차원을 수정하여 겪는 중복 및 메모리 오버헤드를 제거하지만 H(fil)와 W(fil) 차원이 제공하는 추가 재사용을 활용할 수 없는 문제가 남아 있다.

 

2.5 Problems in GEMM-based solutions

분석을 통해 H(fil)와 W(fil)의 컨볼루션 dimensions는 매트릭스 dimensions에 직접 매핑될 수 없다는 것을 알 수 있었다. 이러한 차원을 GEMM으로 표현하기 위해 기존 솔루션은 이전 섹션에서 설명한 대로 오버헤드 또는 처리량 손실을 유발하는 다양한 해결 방법과 수정을 배포한다. 행렬 곱셈이 풍부한 데이터 재사용 기회를 제공하지만, 여전히 컨볼루션 작업이 제공하는 것보다 적다는 점을 고려할 때 이는 불가피하다.

섹션 1에서 설명한 바와 같이, 워크로드 배치의 경우 이러한 오버헤드와 데이터 재사용 손실은 고성능 시스템에서 문제가 되지 않는다. 그러나 메모리 시스템의 기능과 워크로드 크기가 모두 제한된 모바일 시스템에서 GEMM 기반 솔루션의 문제는 무시할 수 없다.